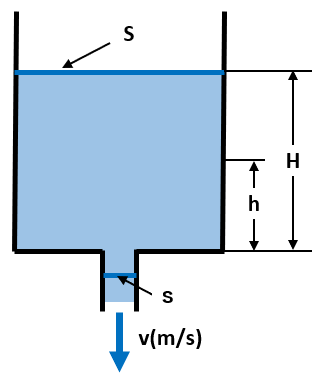
下記の図のような底に小さな穴がある水槽に水が高さがHまで溜められています。
これを排出するときの流出速度と時間を計算します。(比重1.0の水を想定しています)
水面から\( h(m) \)下部にある穴から流速\( v(m/s) \)で水が流出しているとします。
微小時間 \( \varDelta t s \)後、液面の高さは \( \varDelta h(m) \) で減少しますので、以下の式が成り立ちます。
\(−\varDelta hS=vs \varDelta t \) オリフィスの流量係数(cd)※を考慮したトリチェリの定理より、 \(v=Cd\sqrt{2gh}\)となるので、 \(−dhS=Cd\sqrt{2gh}s dt\)で表せます。
従って、t = 0 で h = h1、t = tで h = h2 を境界条件と上式を積分して整理すると以下の通りになります。
\[ t=-\int_{h1}^{h2} \dfrac{S}{Cd s \sqrt{2gh}} \]
\[ =-\dfrac{2S}{Cd s \sqrt{2g}} \begin{bmatrix}h^{1/2}\end{bmatrix}_{h1}^{h2} \]
\[ =\dfrac{2S}{Cd s \sqrt{2g}}(\sqrt{h1}-\sqrt{h2}) \]
※Cd = Ca × Cv で Cd:流量係数、Ca:収縮係数(縮流による損失)、Cv:速度係数(摩擦による損失)
排出量(Q):\( S(H-h ) \)
排出時間(T):\( \dfrac{ 2S } {Cd s \sqrt{2g} } ( \sqrt{H} - \sqrt{h} ) \)
初期流排出速度(Vs):\( Cd \sqrt{2gH} \)
終了排出速度(Ve):\( Cd \sqrt{2gh} \)
重力加速度(g):g=9.81(m/s2)