ハサミムシの扇子

｜ハサミムシの扇子｜サイトマップ｜ホーム｜

ハサミムシは、飛ぶための大きなはねを、普段は背中の下にコンパクトに畳み込んでいます。その収納能力は、広げた時の面積は畳んだ時の約10倍にもなります。
瞬時に展開・収納が可能で、非常に薄い膜でありながら、展開時にはしっかりと形を保持し、飛行に耐える強度を持ちます。
このハサミムシのはねの折れ線を幾何学的に解析し、それを扇子の設計に応用しております。

円Ｐの中心座標：（ｘy）、円Ｐの半径r：

点Ａの座標：（ｘ y）、 織り数：

※x座標は0～100、y座標は0～70で指定してください。

補助線（有無）

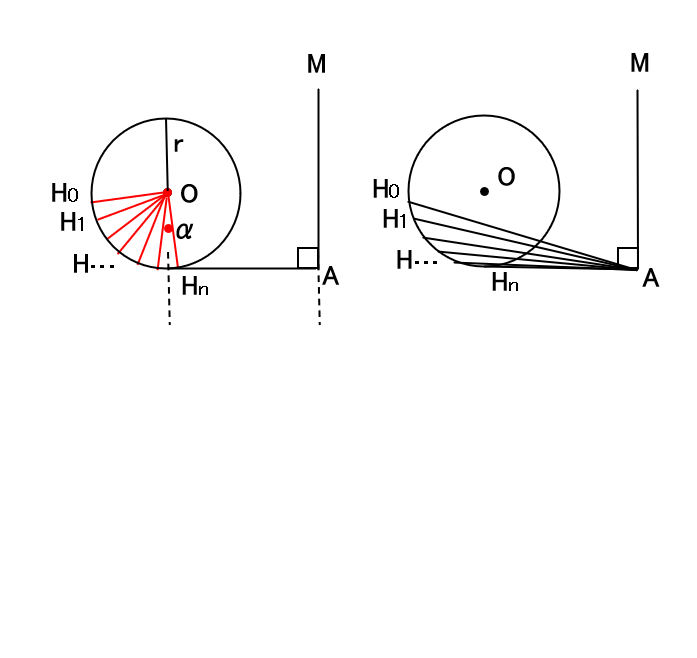
円Ｏを角αでｎ分割した接点をＨ₀～Ｈ_nとします。 Ｈ_nとH_n-1の接点の延長線の点Ａとして、
線Ｈ_nと Ａの直角線上の点をＭとします。
点ＡとH₀～Ｈ_nに引いた線をＡ-Ｈ_ｎとします。

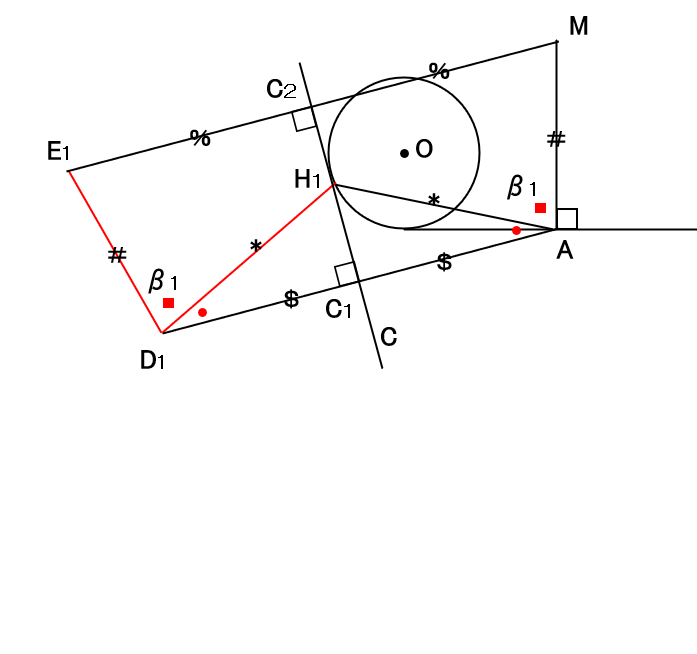
点Ｈ₁とＨ₁₊₁を通る線をＣとして、 Ｃと直角に交わる線をＡ-D₁としてＡ-C₁=C₁-D₁の点を
D₁とします。
Cと直角に交わる線をＭ-E₁としてＭ-C_２=C_２-E₁の点をE₁とします。

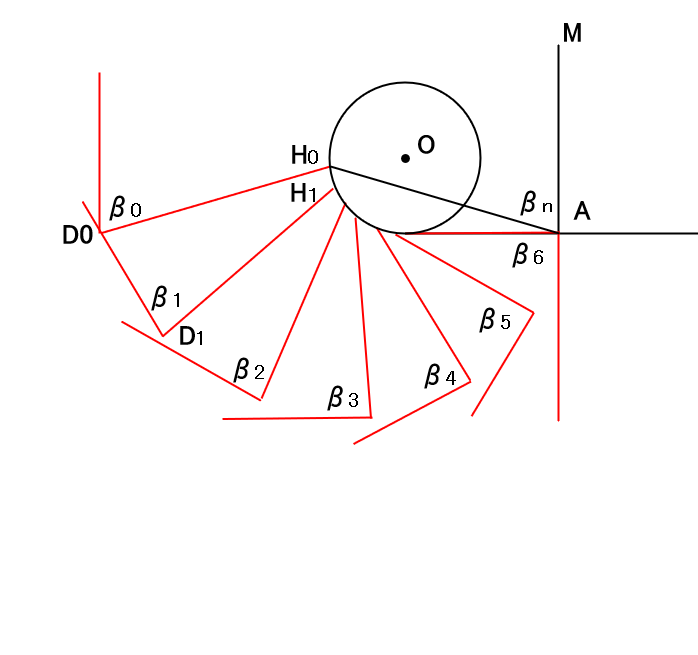
線A-H_n=線H_n-D_n、角H_n-A-M=H_n-D_n-E_n
となるようにＨ₁～Ｈ_ｎまで計算します。

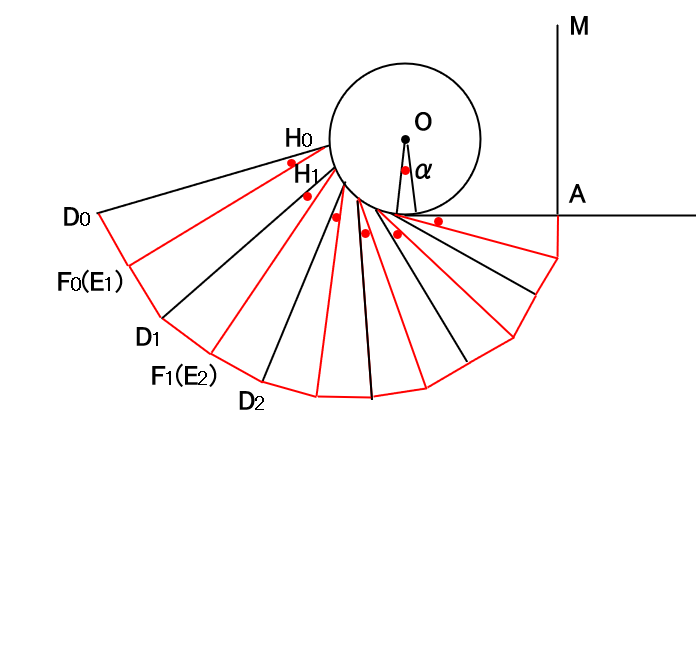
線H₁-D₁と線H₁-F₁を角αとなるように
作成します。
点F₁はD₂-E₂の交点とします。
同様にn=0からｎまで、H_n-F_nをすべて作成します。

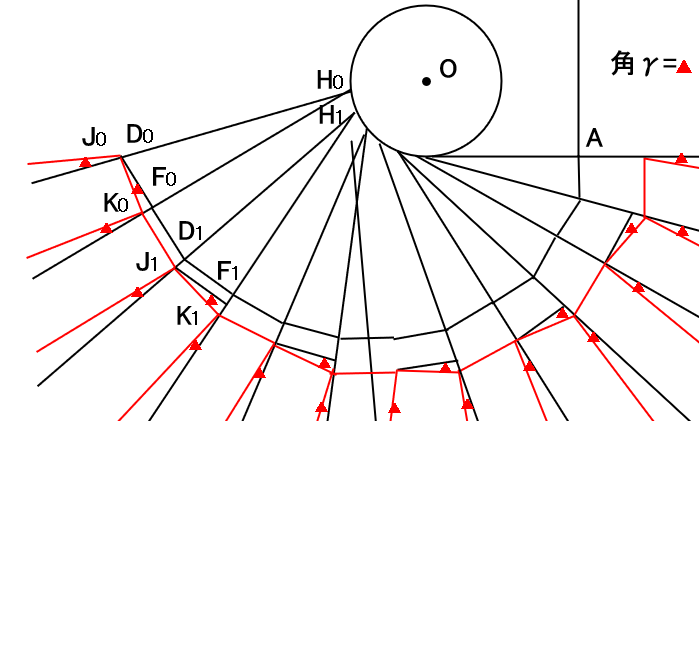
角γは5～10°程度で
ここでは10°に設定

線H_n-D_nの延長線はJnよりγ角ずらします。
線H_n-F_nの延長線はk0よりγ角ずらします。
線J_n-K_nはD_n-F_nよりγ角ずらします。
線K_n-J₁₊₁はF_n-D₁₊₁と並行線とします。
上記の処理をn=0からｎまで作成します。

参考資料：「ハサミムシのファン設計：生体模倣と進化生物学への応用」

｜ハサミムシの扇子｜サイトマップ｜ホーム｜