マンデルブロー集合

複素数列 Z_n = Z_n-1² + C 、Z₀ = 0　が n → ∞ の極限で無限大に発散しないという条件を満たす
複素数 C 全体が作る集合がマンデルブロー集合です。
また、図形の一部をどんなに拡大しても同じような図形が現れてフラクタルな性質があります。

画像の拡大位置をダブルクリックすると中央に位置付けられて図の拡大が出来ます。

マンデルブロー集合は複素数の数列Zで定義され、Zの一般式は
Z_n = Z_n-1² + C 、C = a + b 、Z₀ = 0　で表します。Z_n が発散しないようなCの全体をマンデルブロー集合といいます。
複素数Cをガウス平面（複素数平面）上の1点(a,b)として、あるCを決めたときZ_nを計算し、
その値の発散の有無を定めることでマンデルブロー集合を描きます。
複素数ZをZ_n = X_n + Y_ni として、数列に代入すると
X_n + Y_ni = (X_n-1 + Y_n-1)² + a + bi = (X_n-1² - Y_n-1² + a) + (2X_n-1Y_n-1 + b)i で(i² = -1です)
実数部は　X_n-1² - Y_n-1² + a　虚数部は　2X_n-1Y_n-1 + b　となります。
ガウス平面上(a,b)を定め、X₀ = 0 、Y₀ = 0 を初期値として上の式をｎ回まで反復計算し、
Zの絶対値が発散しないa、bを見つけます。
Zの絶対値√(Xn2 + Yn2) > 2　となると発散すると判定します。
従いまして、実数部はｘ軸-2.0～+2.0、虚数部はｙ軸-2.0～+2.0の範囲で描画します。
反復回数は最大４０回、発散しない場合は黒色表示で、発散と判定した場合は
反復回数（発散の速さ）に応じて色付けして表示しております。



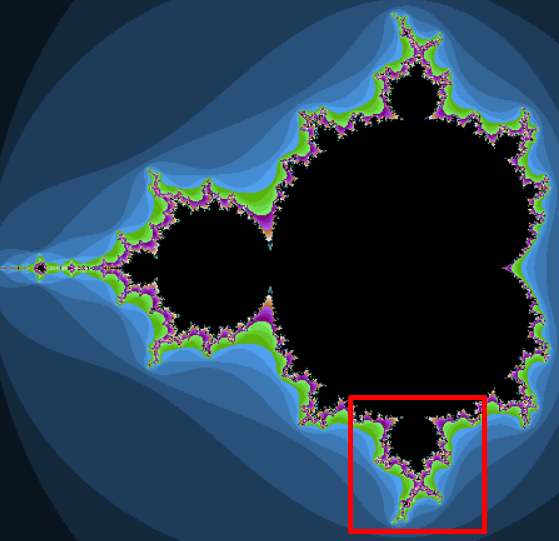
上図の黒く塗られた部分がマンデルブロー集合です。 その一部を拡大したものを真ん中の図、
さらにその一部を拡大したものを右図に示します。
どんなに拡大しても、同じような図形が現れます。このような性質をフラクタルといいます。