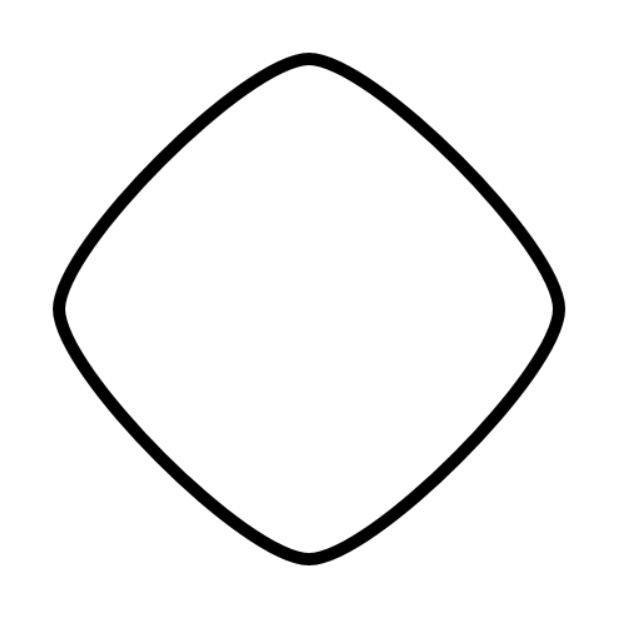
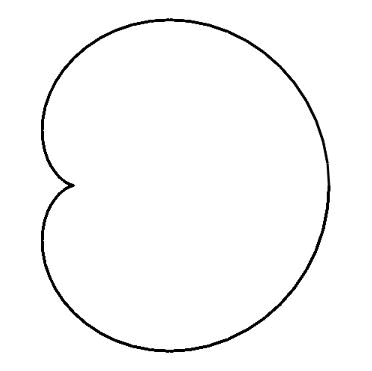
(心臓形)
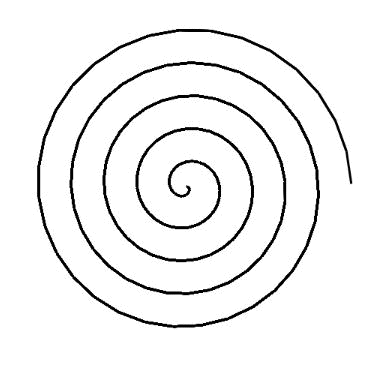
巻きが進んでも巻き幅は変わらないものはアルキメデスの螺旋です。
(星芒形)
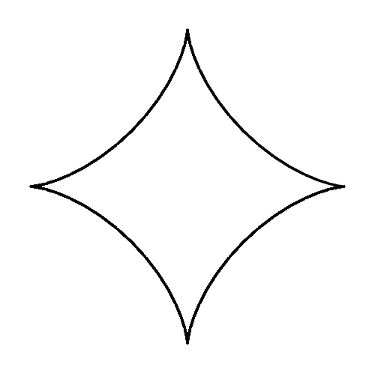
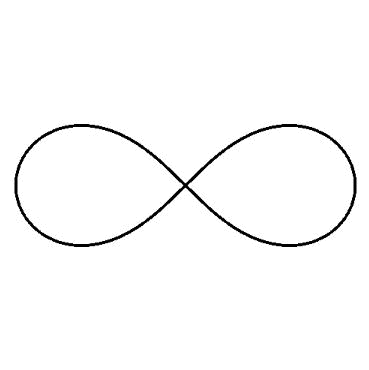
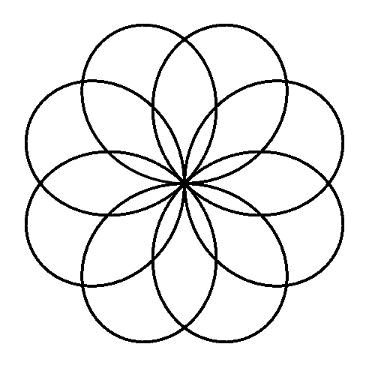
数式の値によってさまざまな図ができます。

定点が描く軌跡として得られる平面曲線の総称です。
一般にサイクロイドといえば定直線上を回転するものを指します。

自然界によく見られる螺旋の一種です。
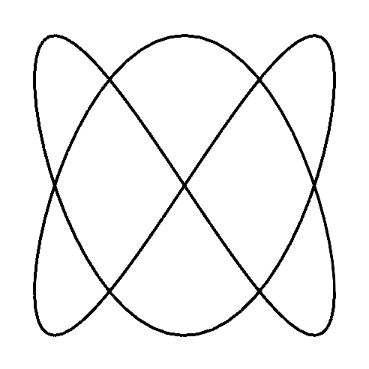
平面図形のことです。
数式の値によってさまざまな図ができます。
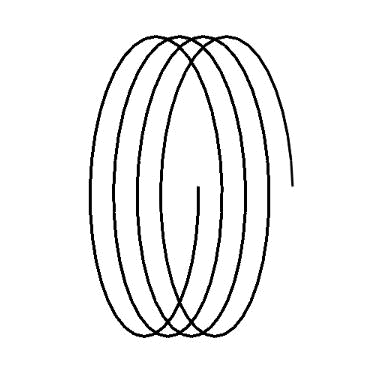
開口部の断面積変化が指数関数的に増加するホーンです。
微妙なラインを簡単に描くことができます。
描画ソフト(Adobe Illustrator、等)やCADソフトなどに使われております。

糸の先端が描く曲線です。
また、機械の歯車に使われている曲線です。
たらしたときに出来る曲線です。
これを上下ひっくり返した曲線がアーチで、建築にも使われています。
また、パラボラアンテナの形は放物線の回転により得られる放物面です。
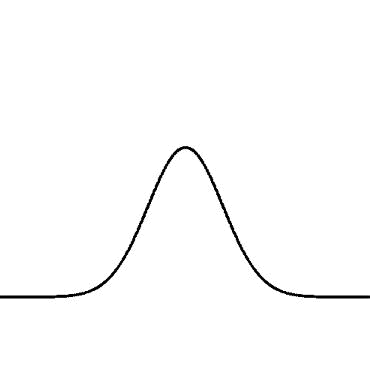
正規分布 に従うと見なせるものが多く、
統計学の理論上も応用上も非常に重要で実用性の高い分布です。
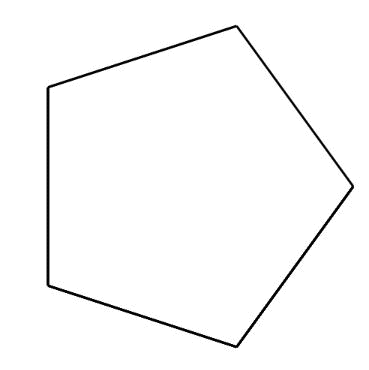
内、全ての辺の長さが等しく、全ての内角の大きさが等しい多角形が正多角形です。
特徴は、どのように回転しても幅が変わらないという特徴を持っています。
応用で、図形のなす角度や、物体の回転角、波や信号のような
周期的なものに対する位相などがあります。
最も近い基地局を探す、新しい基地局の設置場所、散らばったデータの集約、
画像のデータ圧縮などに応用されてます。
操作を無限に繰り返すことによって得られるフラクタル図形の一種です。
正方形同士の接する4つの頂点が直角三角形を形成するため、
ピタゴラスの定理に名を残すピタゴラスの名前を付けております。
これを再帰的に繰り返してできる図です。
中国風のドラゴン(竜)に似ているところから、この名称があります。
それぞれの線分を底辺とする直角2等辺三角形の辺に置き換える操作を
反復的に行うことによって得られる図形です。
左右の枝を幹に置き換えることを繰り返すと出来る図形です。
その別れた2本の枝を基本図形に置き換える操作を続けると、
木の形をした枝分かれ図になります。
平面や空間内の単位正方形、単位立方体を特定のパターンに乗っ取って
全て通るフラクタルな空間補充曲線の一つ.(一本の線で全部のブロックを通るようにする)
空間を覆い尽くす空間充填曲線の一つです。
自己相似的な無数の正三角形からなる図形です。
自己相似的な無数の正方形からなる図形です。
閉曲線であるところに特徴があります。
複素数列 Zn = Zn-12 + C 、Z0 = 0 が n → ∞ の極限で無限大に発散しないという条件を満たす
複素数 C 全体が作る集合がマンデルブロー集合です。
また、図形の一部をどんなに拡大しても同じような図形が現れてフラクタルな性質があります。
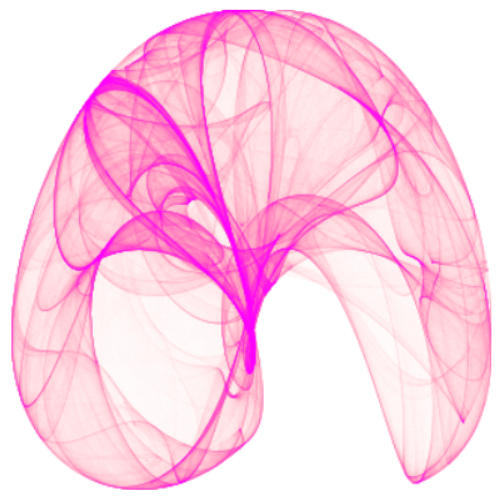
ピーター・デ・ヨング(Peter de Jong)のアトラクターは、特定の数学的な更新規則(写像)を
何度も繰り返すことで描かれる、複雑で美しい幾何学的な図形のことです。
カオス理論の分野では「ストレンジ・アトラクター」の一種として知られております。