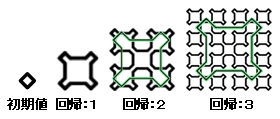
描き方
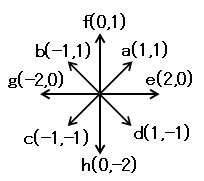
ａ、ｂ、ｃ、ｄ、ｅ、ｆ、ｇ、ｈは次の様なベクトルとすると。
ａ＝（１，１）、ｂ＝（－１，１）、ｃ＝（－１，－１）、ｄ＝（１，－１）、
ｅ＝（２，０）、ｆ＝（０，２）、ｇ＝（－２，０）、ｈ＝（０，－２）
ＡＥＤ、ＢＦＡ、ＣＧＢ、ＤＢＣをそれぞれ
ＡＥＤ：
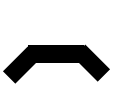：ａｅｄ、
ＢＦＡ：：ｂｆａ、
ＣＧＢ：：ｃｇｂ、
ＤＨＣ：：ｄｈｃ として、回帰数ｎで表すと下記の様になります。
ＡＥＤ（ｎ）＝ＡＥＤ（ｎ－１）・ａ・ＢＦＤ（ｎ－１）・ｅ・ＤＨＣ（ｎ－１）・ｄ・ＡＥＤ
ＢＦＡ（ｎ）＝ＢＦＡ（ｎ－１）・ｂ・ＣＧＢ（ｎ－１）・ｆ・ＡＥＤ（ｎ－１）・ａ・ＢＦＡ
ＣＧＢ（ｎ）＝ＣＧＢ（ｎ－１）・ｃ・ＤＨＣ（ｎ－１）・ｇ・ＢＦＡ（ｎ－１）・ｂ・ＣＧＢ
ＤＨＣ（ｎ）＝ＤＨＣ（ｎ－１）・ｄ・ＡＥＤ（ｎ－１）・ｈ・ＣＧＢ（ｎ－１）・ｃ・ＤＨＣ
初期条件： ＡＣＤ（０）＝””、ＢＦＡ（０）＝””、ＣＧＢ（０）＝””、ＤＢＣ（０）＝””
初期の曲線はａｂｃｄ、回帰１の曲線はａｅｄａｂｆａｂｃｇｂｃｄｈｃｄです。