|
アフィン変換は線形変換(拡大や縮小、回転など)と平行 移動を組み合わせた変換です。
変換前の座標を(x,y)、変 換後の座標を(u,v)とすると下記の様になります。
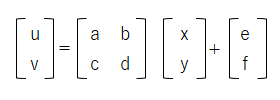
このa〜dの2×2の行列の部分が線形変換、e、fの部分が平行移動の変換を行います。
さらに、3×3の行列を用いて下記の様に表現する場合もあります。
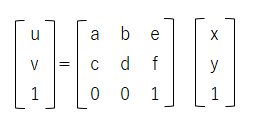
この表現を同次座標と呼び、 線形変換と平行移動とともに行列の積だけで求めることができるので便利です。
拡大/縮小 x軸方向の拡大率をsx ,y軸方向の拡大率をsyとすると、拡大縮小のアフィン変換は下記の通りです。
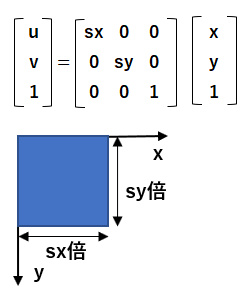 平行移動 x軸方向へtx 、y軸方向へtyだけ移動するアフィン変換は下記の通りです。
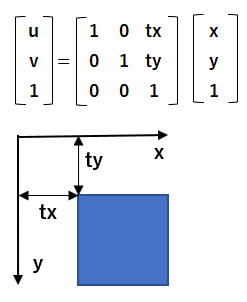 回転 原点回りにθ°回転するアフィン変換は下記の通りです。
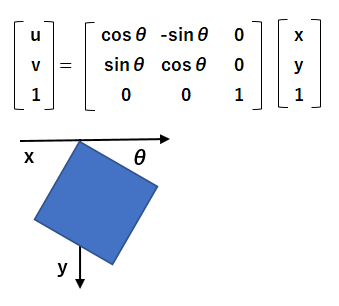 スキュー(せん断) 四角形を平行四辺形に変形する処理をスキューまたはせん断といいます。
x軸に対してθ°y軸方向へ傾ける処理は下記の通りです。
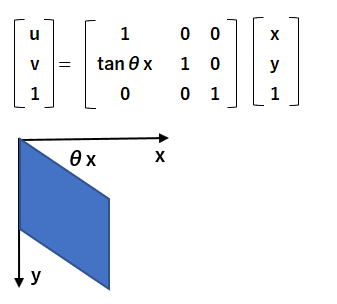 y軸に対してθ°x軸方向へ傾ける処理は下記の通りです。
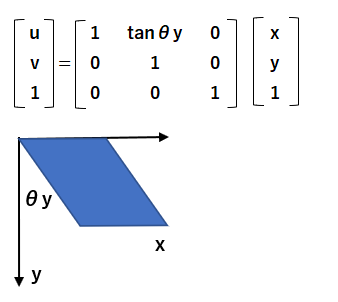
アフィン変換の応用
アフィン変換を平行移動、拡大縮小、回転を組合せて変換の手順を考える必要があります。
として、「変換前 → 平行移動 → 拡大縮小 → 回転 → 平行移動 → 変換後」とします。
画像データを毎回変換するのではなく、アフィン変換行列をまとめて計算して、アフィン変換処理を行います。
具体的には、上記のアフィン変換処理を行列で表すと下記の通りとなり、アフィン変換行列を一回で処理する事ができます。
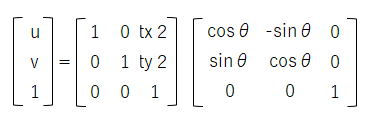 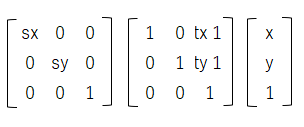
さらに、変換後の座標(u, v)から、変換前の座標(x, y)を求める場合があるのですが、
その時は行列の左側からアフィン変換行列の逆行列を掛けて下記の様に、変換前の座標を求める事ができます。
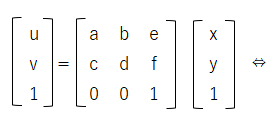 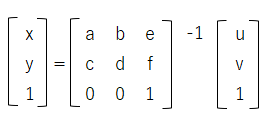
|