射影変換(ホモグラフィ)方法
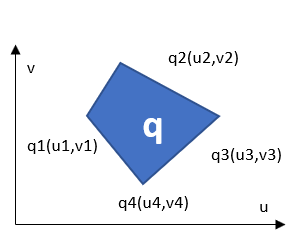
図形pの4点をp1~p4としてx、y座標で表し、図形qの4点をq1~q4としてu,v座標で表します。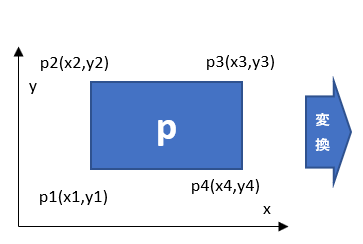
図形pを図形qに変換するときの射影変換の行列式は次のの通りです。
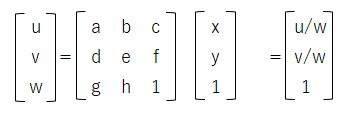
従って、u、vの一般解は次の通りになります。
u = ( ax + bx + c ) / ( gx + hy + 1 )
v = ( dx + ex + f ) / ( gx + hy + 1 )
ax + bx + c - gxu - hyu - u = 0
dx + ex + f - gxv - hyv - v = 0
変換前のp点と変換後のq点の、それそれの4座標を固定すると、
下記の8通りの連立1次方程式が成立ち、a、b、c、d、e、f、g、h の解が得られます。
a x1 + b y1 + c - g x1 u1 - h y1 u1 - u1 = 0
d x1 + e y1 + f - g x1 v1 - h y1 v1 -v1 = 0
a x2 + b y2 + c - g x2 u2 - h y2 u2 -u2 = 0
d x2 + ey 2 + f - g x2 v2 - h y2 v2 -v2 = 0
a x3 + b y3 + c - g x3 u3 - h y3 u3 -u3 = 0
d x3 + e y3 + f - g x3 v3 - h y3 v3 -v3 = 0
a x4 + b y4 + c - g x4 u4 - h y4 u4 -u4 = 0
d x4 + e y4 + f - g x4 v4 - h y4 v4 -v4 = 0
連立一次方程式の解法は、「連立1次方程式の解(ガウスの消去法)」を参照ください。
画像の歪み補正に対する対応
p(x,y)座標からq(u,v)座標へ射影変換して描画すると、画像のドット落ちにより歪みの補正が必要になります。
これを回避するために、描画座標q(u,v)を基準にしてp(x,y)座標を計算して描画するとドット落ちが発生しません。
変換行列の逆行列(x、yをu、vに入れ替えてa~hの値を求める)で座標変換すると対応出来ます。