曲線・図形の書き方（ベジェ曲線）

ベジェ曲線（Bézier Curve）は、N 個の制御点から得られる N - 1 次曲線です。

ベジェ曲線は、フランスの自動車メーカー「ルノー社」の技術者ベジェ氏が、
自動車の設計のために考え出した曲線です。
ベジェ曲線を使えば、コンパスや定規では描けない微妙なラインを簡単に描くことができ、
描画ソフト（Adobe Illustrator、等）やCADソフトなどに使われております。

下のキャンバスのハンドル/アンカーポイント（赤印）をドラックするといろいろな曲線が描けます。

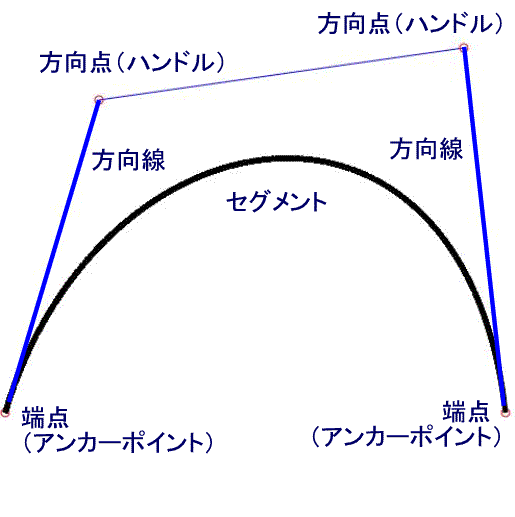
1つのベジェ曲線は、 4つの制御点で構成され、 両端の制御点は端点(アンカーポイント)として、 その間の2点は方向点とします。 端点と方向点を結ぶ線を方向線と呼びます。 端点から端点の線をセグメントと呼びます。 方向線はアンカーポイントから出る セグメントの方向と強さを決めます。 方向点（ハンドル）の操作で色々な曲線が描けます。
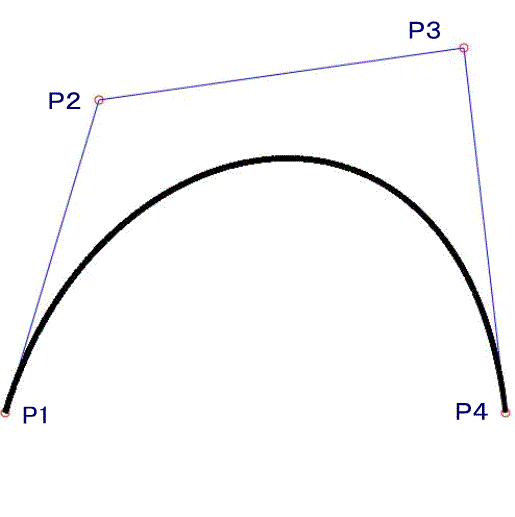
端点をＰ１、Ｐ４とし 方向点をＰ２、Ｐ３とします。
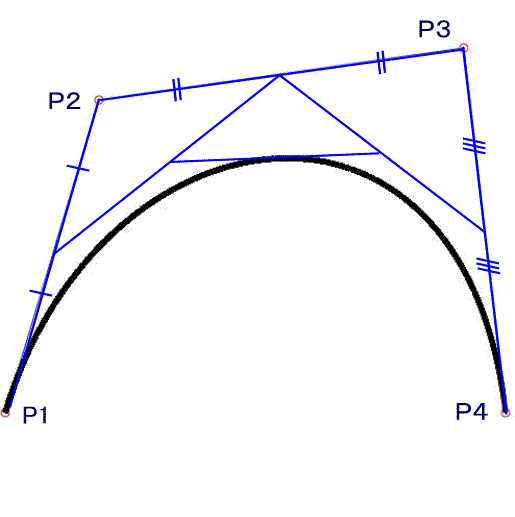
P1とP2、P2とP3、 P3とP4を直線で結びます。 それぞれの直線を2分割し、 分割点を直線で結びます。 この分割を繰り返します。 分割数を多くすれば、 分割点はベジェ曲線となります。
それぞれの点を右図の通りｘ，ｙ座標として、 数式でベジェ曲線を表現すると x = (1-t)3x1 + 3(1-t)2tx2 + 3(1-t)2x3 + t3x4 y = (1-t)3y1 + 3(1-t)2ty2 + 3(1-t)2y3 + t3y4 で示します。