1.平面敷詰可能な図形
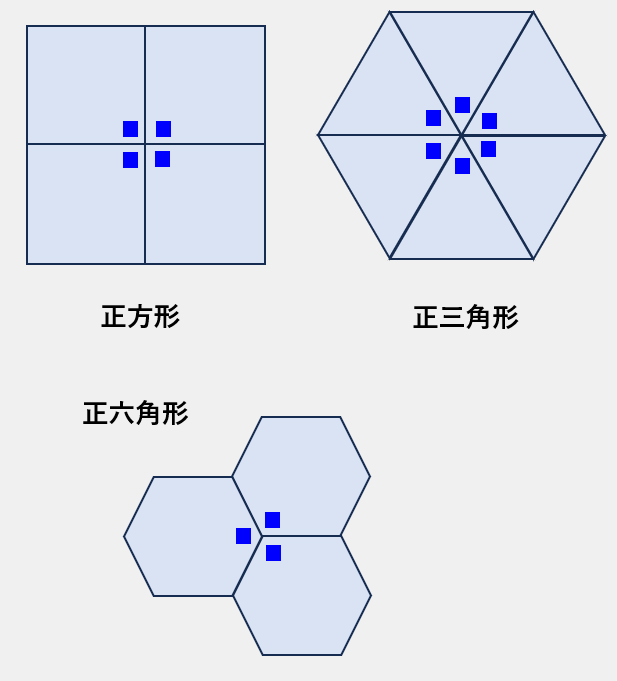
(1)正多角形
正三角形、正方形、正六角形は、いずれも頂点の周りの内角の合計が360度になるため、平面に敷詰めることが可能な図形です。
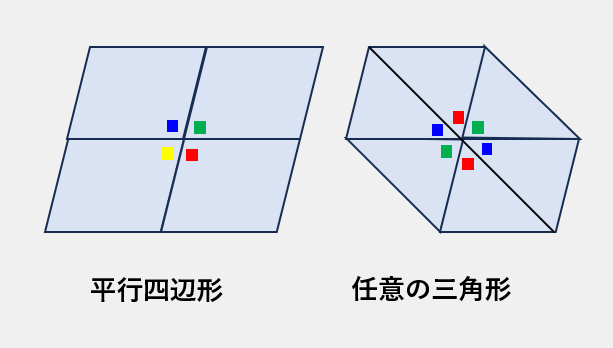
(2)平行四辺形/任意の三角形
平行四辺形も内角の合計が360度になるため、平面に敷詰めることが可能です。
さらに、平行四辺形を対角線で分割した任意の
三角形も同様に平面敷詰可能形です。
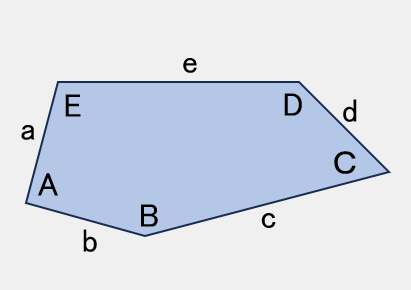
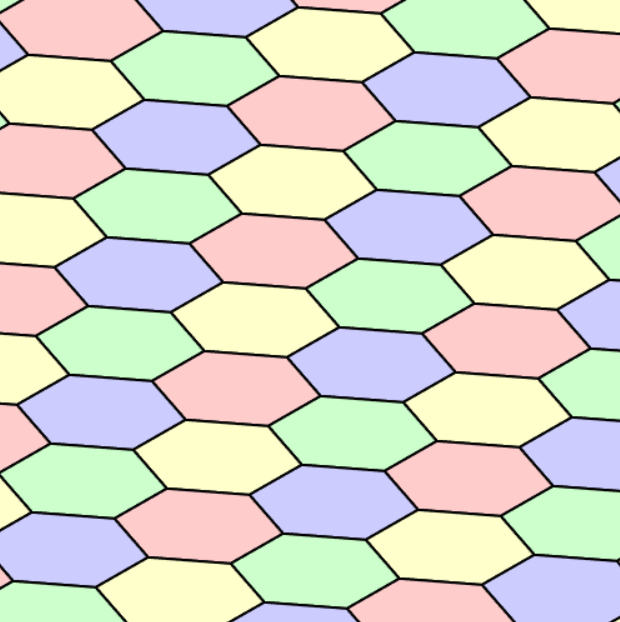
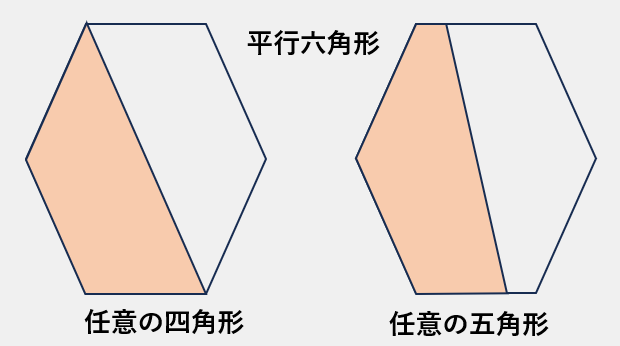
(3)平行六角形
平行六角形も平行四辺形と同様に平面敷詰可能な図形です。
これを、対角線線で分割すると、その線の中心点で点対称な
任意の四角形に分割できます。
また、向い合う2辺を任意に分割して、その分割点より引いた線で
出来た任意の五角形に分割出来ます。
それぞれの任意の四角形・五角形は平面敷詰可能な図形です。
(4)その他応用
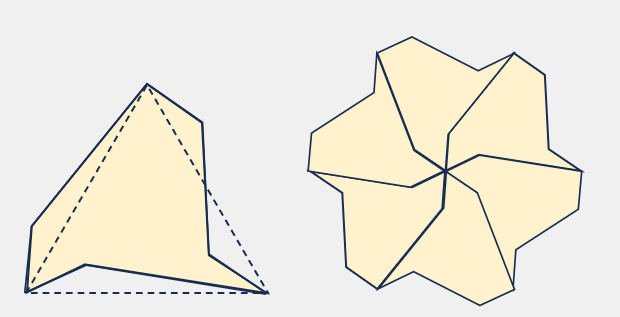
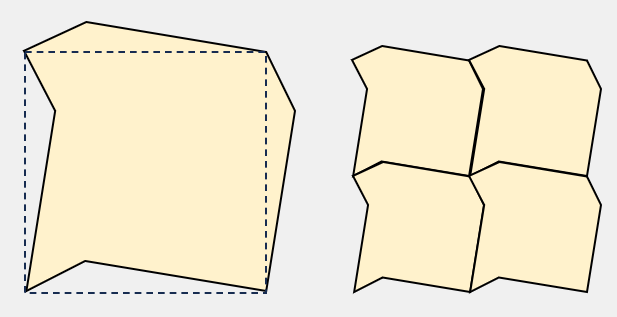
正三角形の応用で、頂点引かれた2辺の
点対称な「くの字」の線とそれ以外の辺を
「ヘの字」で左右対象に引いた線で作られた任意の
七角形は平面敷詰可能な図形になります。
また、任意の線で作られた図形も平面敷詰可能です。
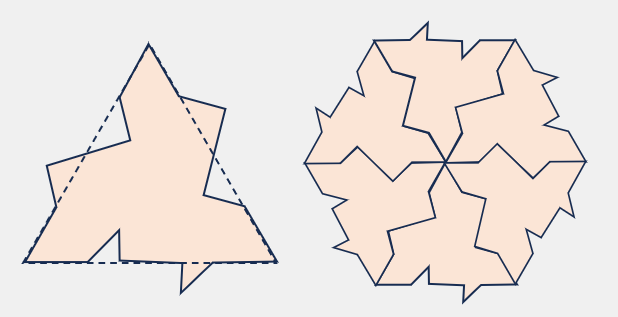
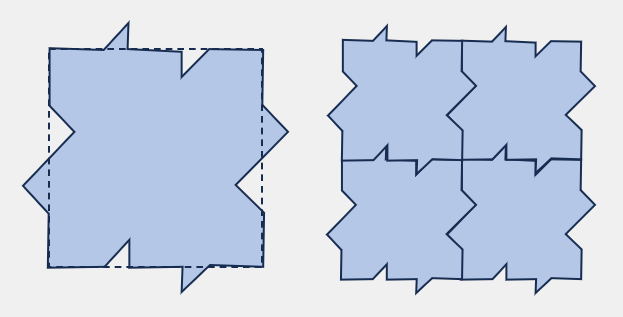
正方形の応用で、それぞれ向い合う辺を
「ヘの字」で引いた線で作られた任意の
八角形も平面敷詰可能です。
こちらも、任意の線で作られた図形は
平面に敷詰めることができます。
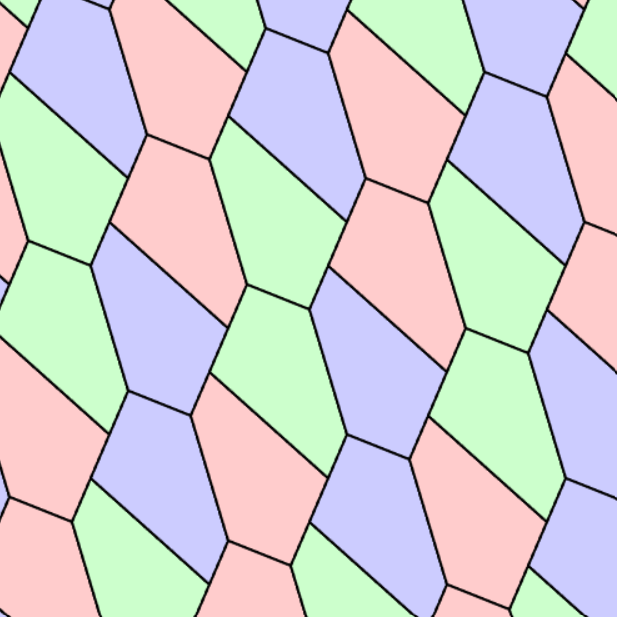
2.平面敷詰可能な凸五角形
平面敷詰可能な凸五角形は15種類しか存在しないとされています。
これについては、凸五角形敷詰図形を調べて描画しました。
描画条件については、「凸五角形タイル張り問題」のサイトを参考にさせて頂きました。
基本の図形は図形の形状を設定して「図形の描画(自作)」ツールで作成して敷き詰めております。
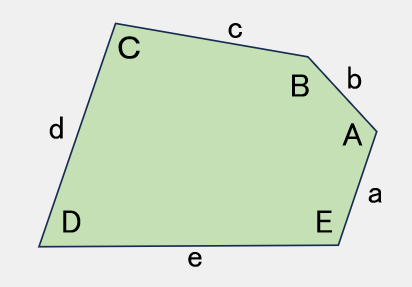
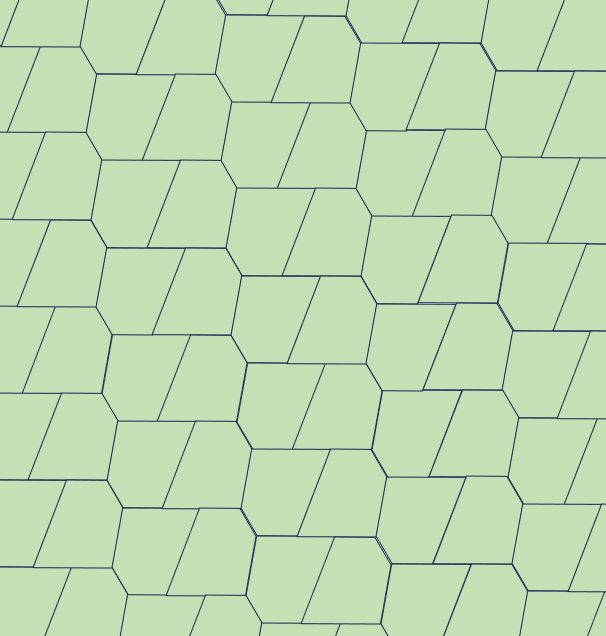
TYPE 1
A+B+C=360°【参考値】
A=120°,B=140°,C=100°
a=100,b=80,c=150,d=200
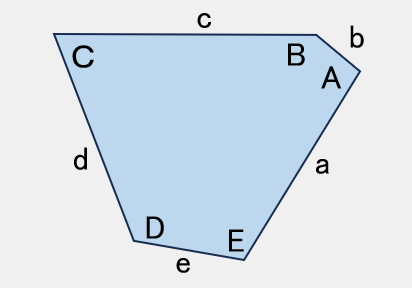
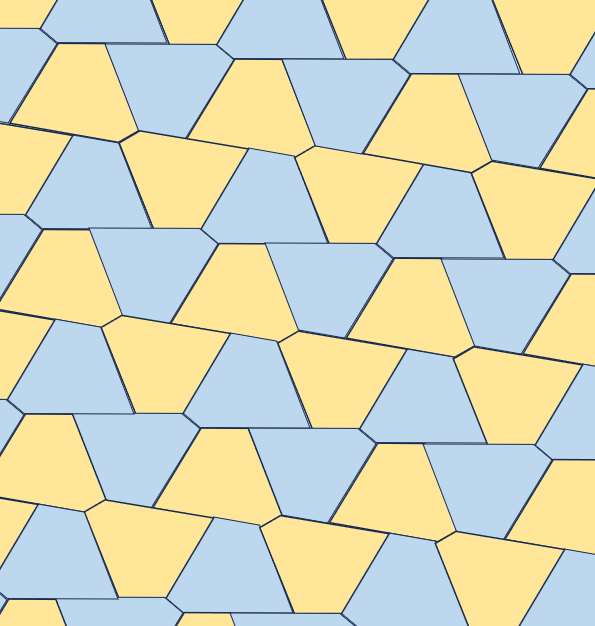
TYPE 2
A+B+D=360° ,a=d【参考値】
A=100°,B=140°,D=120°
a=200,b=50,c=230,d=200
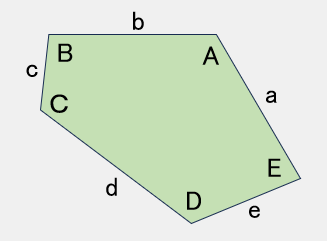
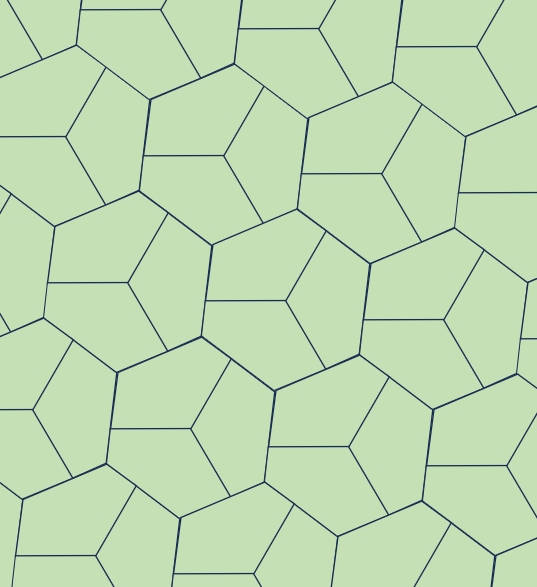
TYPE 3
A=C=D=120° ,a=b,d=c+e【参考値】
E=83°
a=b=200,c=90,d=229
e=139
TYPE 4
C=E=90° ,a=e,c=d【参考値】
A=130°,D=150°
a=100,b=215,c=175,
d=175,e=100
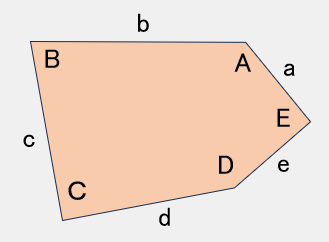

TYPE 5
A=120°,C=60°,a=b,c=d【参考値】
B=130°
a=b=150,c=d=200
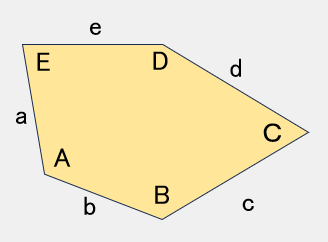

TYPE 6
A+B+D=360°A=2C a=b=e,c=d
【参考値】
A=86°,B=152°,
C=43°,D=122°
a=b=e=87,c=d=200
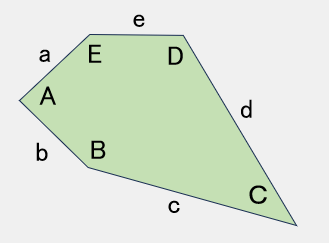

TYPE 7
2B+C=360°,2D+A=360°a=b=c=d
【参考値】
A=130°,B=136°,
C=88°,D=115°
a=b=c=150
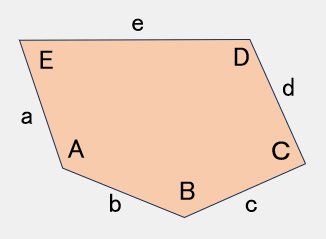
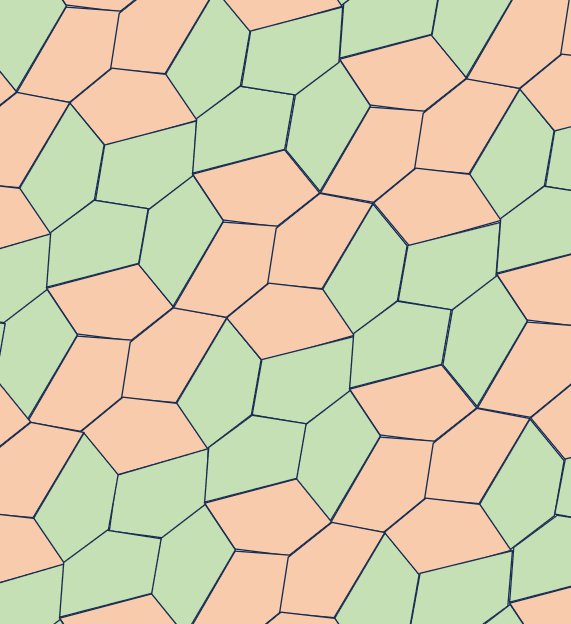
TYPE 8
2A+B=360°,2D+C=360°a=b=c=d
【参考値】
B=154°,C=56°,
D=152°,A=103°
a=b=c=d=150
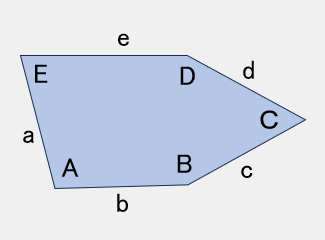
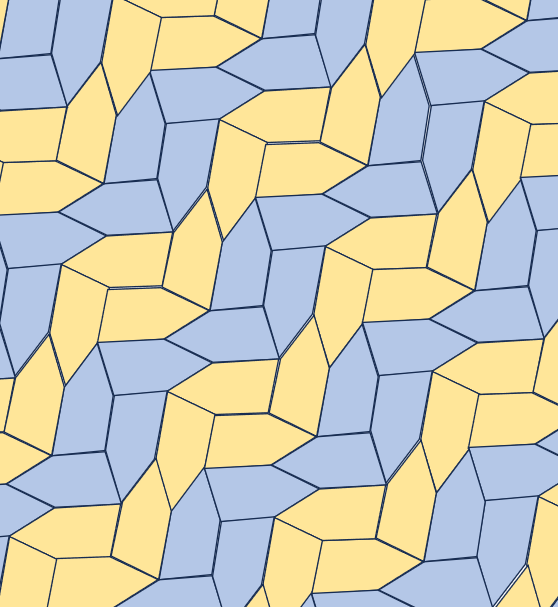
TYPE 9
2E + B = 360°2D + C = 360°
a = b =c = d
【参考値】
B=131°,C=70°,
D=145°,E=114,5°
a=b=c=d=200
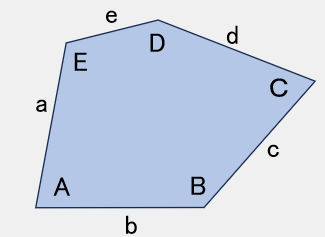
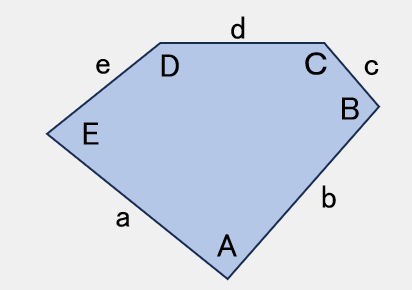
TYPE 10
A = 90° ,B + E = 180°2D+E=360° ,2C+B= 360°
a=b=c+e
【参考値】
B=100°,C=130°,
D=140°,E=80°
a=b=200,c=74,e=126

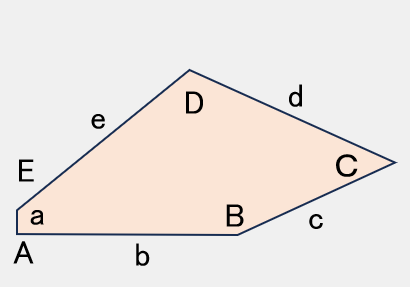
TYPE 11
A = 90° C + E = 180°2B + C = 360°
d = e = 2a + c
【参考値】
B=155°,C=50°,
D=115°,E=130°
a=22,c=156,d=e=200

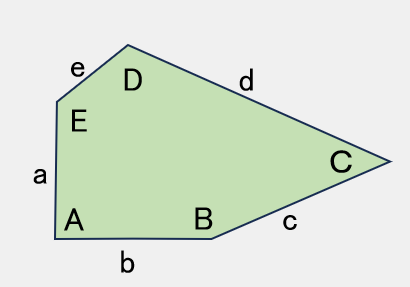
TYPE 12
A = 90° ,C + E = 180°2B + C = 360°
2a = d = c + e
【参考値】
B=155°,C=50°,
D=115°,E=130°
a=100,c=135,d=200,e=65
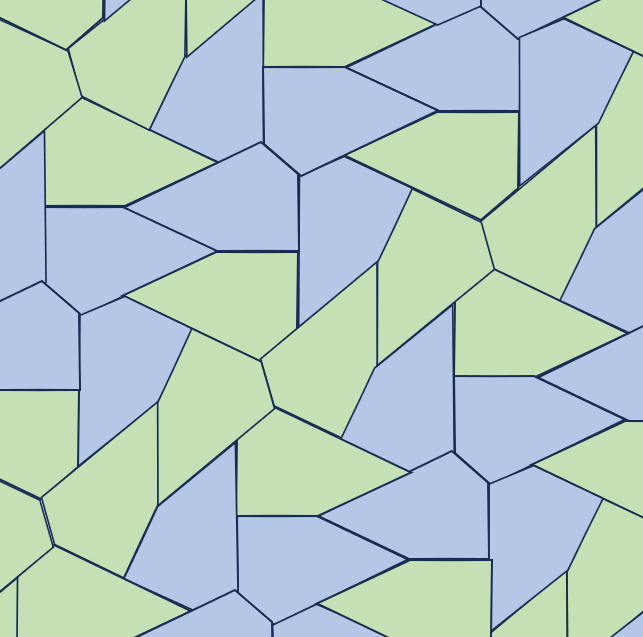
TYPE 13
A = C = 90°2B = 2E = 360°- D
2c = 2d = e
【参考値】
B=110°,D=140°,E=110°
c=d=100,e=200
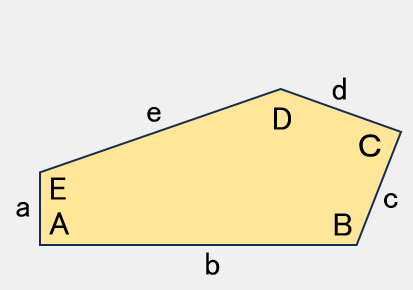

TYPE 14
A = 90° ,C+E = 180°2B+C= 360°
2a=2c = d = e
【参考値】
B=145.5°,C=69°,E=111°
a=c=100,d=e=200
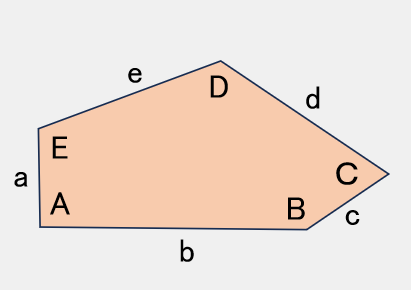
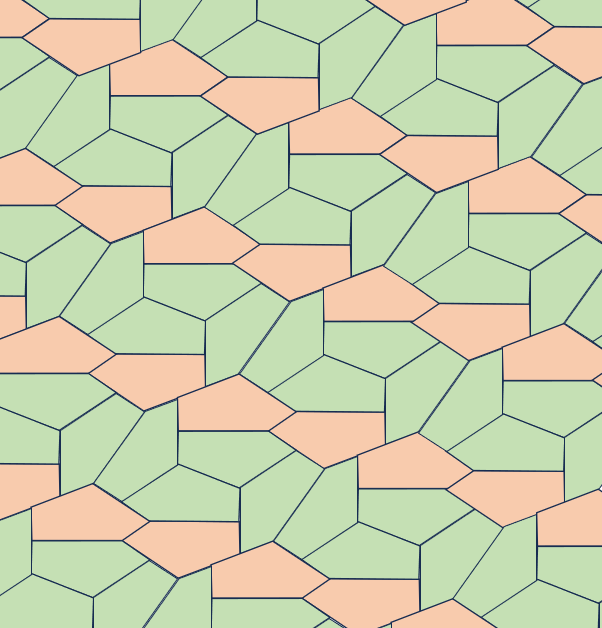
TYPE 15
A = 90°,E=150°,C=60°2a = 2b = 2d=c
【参考値】
B=150°,D=135°
a=b=d=100,c=200